深夜に佐藤青児先生から以下のメッセージをいただきました。
「http://ameblo.jp/ddwts503/entry-12225792822.html
筋膜の張力は 屈筋伸筋の任意の力で決めることができその張力によって 水が 屈筋の伸展方向に伸びる多大な 推進力になると思うのですがその力を 計算式で書けないか?と思っています。一度考えてみてください。」
さっと読んだ第一印象は「???」
引用されているブログをによると佐藤先生「熱にうなされながら 頭の中で 屈筋の張力にたいする筋肉の伸長方向への斥力を計算できないか? と思っていたのですがなんとなくおぼろげながら 計算できそうで できなくてって感じで それを 動画でとってみました」
佐藤先生、熱でうなされているときでも筋肉の命題について考察するんだ〜〜!凄いなあ。
私が博士論文を書いていた頃、指導教官に「もっと研究に没頭しろ。研究内容か夢に出てくるくらいじゃないと博士号は取れないぞ」と叱咤激励されたことを思い出しました。
佐藤先生はきっと寝ても覚めてもリンパケアの事を頭のどこかで考えてるんだろうなぁ。
まさしく研究者!
いただいたお題にどうお答えすればいいか?何を聞かれてるのかを理解するまでに、メッセージとブログを何度も黙読し、最終的には音読し、動画もリピート。
腕のサムラインを何度も進展させて考察しました。
で、 私
「先生の「斥力」は「筋肉が伸展する方向に働く力」という理解でいいでしょうか?それでしたら「伸展力」の方がより正確に伝わるかと思います。 伸筋が縮み、拮抗して屈筋が伸展することで屈筋の筋膜が伸展する。この時の筋膜が張力を持つことで屈筋を筒状に整え、その筒状の筋肉の断面積を小さくする方向に働く。この時に屈筋の中心部から端に押し出された水が屈筋の「伸展力」として作用する。 先生のお考えを定性的に言葉でまとめると上記の理解でいいですか? これを式に起こすには屈筋の断面積の変化を、それに垂直する方向に働く力に変換する式が要な気がします。いかがでしょうか?」
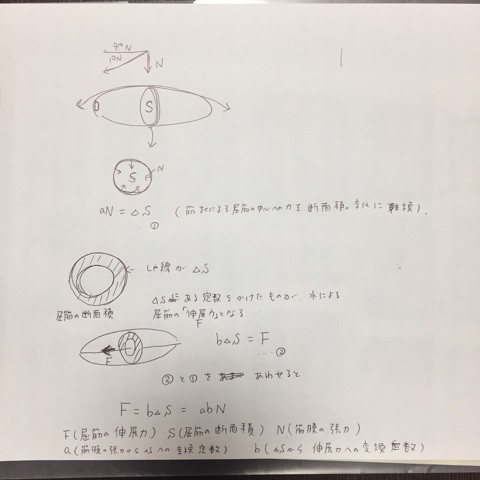
こんなお返事した後に佐藤先生が以下のようにブログに書いていたことに気がつきました。 佐藤先生「筋膜内にかかる圧力は パスカルの法則で一定ですですから 圧力がかわるということはありません
ただケチャップや マヨネーズのように周囲の太いところに力をかけると 細いところから
勢いよく飛び出るそのイメージなんですね
なんとか 筋肉の油圧ポンプ力の検証が 数学的にできないのか?
とにかく 筋肉は 筋膜の伸展によって張力を自由に変化させることができそれが 直接 伸展力になることは確かなのです。
筋膜内圧を高めていけば それが 筒状になり ポンプ圧になる」
とのことで、私のお返事いい線いったと思いますが、きっと、先生の知りたいことは、私の立てた式のaとbの中身なんだろうなぁ。
私のお返事へのお答えは
佐藤先生「ありがとうございます!
縦のちからが 縦の力の推進力になることの
証明をなんとかできると面白いです。」とのこと。
佐藤先生はここからどんな解を導き出すのかしら?楽しみにしてますね!
コメントを残す